BASICAS E I N G E N I E R í A

(1)

UNIVERSIDAD

A U T ~ N O M A

M E T R Q P O L I T A N ~

u

NI D A D

I

Z T A P A L A P A

D l V l S l Ó N D E C I E N C I A S

BASICAS

E I N G E N I E R í A

I N G E N I E R í A E N E L E C T R ó N I C A E N C O M U N I C A C I O N E S

PROVECTO

TERMINAL

C O D I F I C A D O R

-

DECODIFICADOR

C O R R E C T O R D E

ERRORES

REED

-

SOLOMON

PROFESOR:

ALUMNOS:

MORALES CORONA TERESA c2L Z 2 O iG '3

(2)

I N D I C E

Temas: Pagina

Introducción. Obietivo. Antecedentes.

Códigos AlfanumBricos. Código ASCII.

Caracteres del código ASCII extendido. Códigos con aplicaciones a control. Cubos-N y distancia.

Códigos para detectar y corregir errores. Códigos detectores de errores.

Códigos para corrección de errores y detección de errores múltiples. Códigos de Hamming.

Códigos de suma de verificación. Códigos m de n.

BCH.

Código Reed-Solomon.

Modelo de un Sistema de Comunicaciones. Detección de errores.

Redundancia.

Corrección de errores.

Objetivos de la Transmisión Digital de la Información.

Codificación del canal.

(3)

Campos Finitos {Campo de Galois}.

Generación de un Campo de Galois (q).

Código Reed-Solomon. Algoritmo Teórico.

Codificación. Canal.

Polinomio de erratas.

Calculo de Síndromes.

Calculo del polinomio localizador de borrados

z(x)

.

Calculo de los síndromes de Forney,

T(x)

.

Algoritmo de Berlekamp (calculo de ~ ( x ) ) .

Calculo de las raíces inversas de

~ ( x ) ,

búsqueda de Chien. Calculo de valores de erratas.

Ejemplo prclctico con un RS(75,9 ), donde

n

= 15 y

k

=

9 .

Decodificación.

Implementación en hardware de un codec corrector de errores Reed-Solomon. Codificador.

Interfaz. Decodificador.

Figura 12. Esquema del Codificador. Figura 13. Diagrama del Codificador. Figura 14. Control del Codificador.

Figura 15. Buffer usado para contaminar la informaci6n. Figura 16. Diagrama de la lnterfaz Serie

/

Paralelo. Figura 17. Esquema del Decodificador.

21 21 23 23 24 24 25 25 25 25 25 25 26 26

26

36 36 41 42 46 47 49 50 51

48

(4)

Codificador y decodificador corrector de errores Reed-Solomon

En la transmisión desde naves espaciales o a través de satélites de comunicaciones se emplea la teoría de códigos correctores. Como ejemplo podemos mencionar

el

Mariner

4

cuando en

1965

envió a la Tierra las primeras imágenes

del

planeta Marte, a pesar del gran avance,

las

fotografías recibidas, comparadas con las de hoy día carecían de alta calidad. Poco después

(1

969-72)

los Mariner

6, 7

y

9

enviaron a la tierra nuevas imbgenes, las im6genes enviadas fueron de gran calidad comparadas con las primeras, pero no se asemejan a la calidad actual. La razón principal de esta mejora fue que para la transmisión de las últimas se había utilizado un potente código corrector, capaz de corregir hasta

5

bits erróneos de cada secuencia de 32. Los grandes avances actuales en la transmisión digital no serían posibles sin el desarrollo de los códigos correctores,

el

teléfono móvil, la televisión digital, los sistemas de navegación aérea,

...

deben en buena parte su éxito al uso sistem6tico de sistemas de codificación que, mediante el uso de una cierta redundancia en

la

informacih a transmitir, consiguen recuperar la información esencial aún cuando las condiciones de la transmisión sean sumamente adversas.

(5)

O

B

J

E T I V O

(6)

ANTECEDENTES

Los circuitos electrónicos básicos procesan las señales analógicas mediante combinaciones de dos estados que podemos llamar

O

y

1

(cada estado representa un

bit),

a

estas combinaciones

de

bits les asignamos una representación determinada, como podría ser el caso de tomar

2

bits y representar con la combinación de ellos los números decimales

O,

1 ,

2

y

3 de la siguiente forma el

O

decimal corresponde a la combinación de bits

00,

el

1

decimal a la combinación

O1

,

el

2

decimal a

1 O

y

el

3

decimal a

1 l .

En general podemos decir que un conjunto de cadenas de n bits ordenados según un patrón Único, en el que las diferentes cadenas de bits representan diferentes tipos de información como pueden ser números, letras, u otros símbolos se llama

CODIGO,

puede que haya o no alguna relación aritmética entre los valores de los bits en una palabra de código y

lo

que representa.

Ejemplos de algunos códigos existentes:

Código decimal

BCD

(decimal codificado binario), que codifica los dígitos por sus representaciones binarias sin signo de

4

bits del

O000

al

1 O01

,

y las palabras del código restante no se usan

(1

O1 O

al

1 1 1

l),

el código Gray, es un código sin pesos y no aritm6tico; es decir un código sin valor ya que las posiciones de los bits en los grupos de código no tienen ningún valor especifico asignado por la posición, que pertenece a una clase de códigos llamada códigos de cambio minirno, en los cuales sólo un bit

del

grupo de código cambia cuando pasa de una palabra a la siguiente, es decir sólo varía un bit de un código

al

siguiente cambio, este código se usa en dispositivos de entrada y salida y en algunos tipos de convertidores de analógico a digital.

Códigos Alfanumbricos

Además de números es necesario manejar información de tipo texto, como

lo

son las letras del alfabeto, signos de puntuaci6n y símbolos especiales, estos códigos se denominan códigos alfanuméricos. Como mínimo un c6digo alfanum6rico debe poder representar los

10

dígitos decimales, y

las

26

letras del alfabeto es decir al menos

36

elementos lo que requiere mínimo

6

bits, pero como deben poder representarse letras mayúsculas y

(7)

de puntuación y entre

20

y

40

caracteres más, cómo

+,

/,

#,

-,

*,

%,

etc. Esta cantidad requiere

7

bits para cada combinación de código, con

lo

que existen

128

posibles combinaciones.

El código

ASCII

es el código alfanumérico más usado.

Código

ASCII

El código de caracteres más comúnmente usado, por ser universalmente aceptado es el

código

ASCII

(American Standard Code for Information Interchange, código estándar americano para el intercambio de información). Este código dispone de

128 caracteres que

se representan mediante un código binario de

7

bits. Los primeros 32 caracteres ASCII son comandos no gráficos, que nunca se imprimen o presentan en pantalla, y solo se utilizan para propósitos de control. Los demás caracteres son símbolos gráficos que pueden imprimirse o mostrarse en pantalla, e incluyen las letras

del

alfabeto (mayúsculas y minúsculas), los

1 O

dígitos decimales, los signos de puntuación y otros símbolos comúnmente utilizados.

Caracteres del código

ASCII

extendido

Además de los

128 caracteres estándar, existen

128 caracteres adicionales que fueron

adoptados por

IBM

para utilizarlos en sus computadoras. Debido a que estos caracteres del código ASCII extendido se usan también en otras aplicaciones distintas a las de la computadora, este código extendido se ha convertido en un estándar no oficial.

El

código

ASCII

extendido está formado por caracteres que pertenecen a las siguientes categorías:

0 Caracteres alfabéticos no ingleses. Símbolos no ingleses.

Letras griegas Símbolos matemáticos. Caracteres para gráficos. Caracteres grcificos de barras.

0 Caracteres sombreados.

Códigos con aplicaciones a control

No

todos las palabras codificadas representan datos, en los sistemas digitales a menudo se encuentran aplicaciones en donde una cadena de bits es usada para controlar una acción, para verificar una condición o para representar el estado presente del hardware, el código que más se usa para estas aplicaciones es el código binario simple.

Si

hay n

(8)

Codificador y decodificador corrector de errores Reed-Solomon

Pero un código binario a pesar de tener en cada palabra el menor número de bits no siempre es la mejor elección para codificar acciones, condiciones o estados.

Cubos-N y distancia

Una cadena de n bits puede visualizarse geométricamente, como un vértice de un objeto llamado cubo n, la figura

1

muestra cubos n para

n = l , 2 , 3

y

4.

Un cubo n tiene

2"

vértices, cada uno de los cuales esta rotulado con una cadena de n bits. Las aristas se dibujan entre vértices adyacentes cuyos rótulos difieren del vértice dado en

solo

un bit. M6s a116 de n=4, los cubos n son realmente difíciles de dibujar.

10

1 1

O

Cubo 1 1

60 dl

cubo 2

cubo 3

1 l J 0 1 1 1 1

01)

o

01.1 1 l q l ó l o p

o o p

-~ OQl 1 1 1'00

, 1 i o 1

o y o

1

a b -

1600 1601

'Figura l. cubos n para n= 1,2,3 y 4

Para valores razonables de n,

los

cubos n facilitan la visualización de ciertos códigos y de los problemas de minimización lógica. Por ejemplo, el problema de diseñar un código Gray de n bits es equivalente a encontrar una ruta a

lo

largo de los vértices de un cubo n ,

(9)

que visite cada vértice exactamente una vez.

A continuación se presentan

la figura 2 con las rutas para

los

códigos Gray de 3 y

4

bits.

110 _.. 1 1 1 _..

o 1 _{. . . ~}

o

o1

1

~ ~

.

1 O0 _0-

1 6 1

'Figura 2. Recorrido en orden del c6digo Gray (a) cubo 3, (b) cubo 4

Los

cubos también proporcionan una interpretación geométrica para el concepto de distancia también llamada

la

distancia de Hamming.

La

distancia entre dos cadenas de n bits es el número de posiciones de bits en que difieren. Para un solo cubo n, la distancia es

la

longitud mínima de una ruta entre los dos vértices correspondientes. Dos vértices adyacentes tienen distancia

l .

Los

vértices

O01

y

1 O0

en el cubo

3

tienen distancia

2. El

concepto de distancia es fundamental en e l diserío de los códigos detectores de error.

Un subcubo m de un cubo n es un conjunto de

2"'

vértices en los que n-m de los bits tienen el mismo valor de cada vértice y los restantes m bits toman todas

las

2"'

combinaciones. Por ejemplo,

los

vértices

(000, O1 O,

100,

1 1 O)

forman un subcubo

2

de un cubo

3.

Este subcubo puede también denotarse con una sola cadena

xx0,

donde "xN denota que ese

bit

particular toma cualquier valor y es llamado un no importa; cualquier vértice cuyos bits coinciden en

las

posiciones que no son x pertenece a este subcubo.

El concepto de

subcubos es particularmente útil para visualizar algoritmos que minimizan el costo de funciones lógicas combinacionales.

(10)

Códigos para detectar y corregir errores.

Un error en un sistema digital es la distorsión del valor correcto del dato, a algún otro valor. Un error es ocasionado por una falla física. Las fallas pueden ser temporales y permanentes. Por ejemplo, un rayo cósmico puede ocasionar una falla temporal de un circuito de memoria, cambiando el valor de un

bit

almacenado ahí. Permitir que un circuito se caliente demasiado o se dañe con la electricidad estática puede ocasionar una falla permanente, de modo que ya no trabaje correctamente.

Los efectos de las fallas en

los

datos se predicen mediante los modelos de error.

El

modelo de error mds simple, se llama el modelo de error independiente. En este modelo se supone que una sola falla física afecta solo a un bit de los datos; el dato distorsionado se dice que contiene un error individual. Múltiples fallas pueden ocasionar errores múltiples, dos o m6s bits erróneos, pero se supone que los errores múltiples son menos probables que los errores individuales.

Códigos detectores de errores

Recordando que un código que usa cadenas de n bits no necesita contener

2"

palabras de código validas; este es el caso de los siguientes códigos. Un código detector de error tiene la propiedad de que la alteración de una palabra de código probablemente producirá una cadena de bits que no es una palabra de código.

Un sistema que usa un código detector de errores genera, transmite y almacena sólo palabras de código. Por lo tanto, los errores en una cadena de bits pueden detectarse mediante una regla simple, si la cadena de bits es una palabra de código, se supone que es correcta; si no es una palabra de código, 6sta contiene un error.

Un código de n y sus propiedades de detección de errores bajo el modelo de error

independiente puede explicarse fácilmente en términos de un cubo n. Un código es simplemente un conjunto de los vértices del cubo n.

A

fin de que el código detecte todos

los

errores individuales, ningún vértice de palabra de código puede ser inmediatamente adyacente a otro vértice de palabra de código.

(11)

do0

O0

1

110 O00

O0

1

0 Palabra de código

X Palabra que no pertenece al código

'Figura 3. Palabras de código en dos códigos de 3 bits diferentes; (a) distancia mínima= 1, no detecta todos los errores individuales ; (b) distancia minima=2, detecta todos los errores individuales.

Un código detecta todos los errores individuales si la distancia minima entre todos

los

pares posibles de palabras del código es

2.

En general, necesitamos n + l bits para construir un código detector de errores individuales con

2"

palabras de código. Los primeros n bits de una palabra de código, llamados bits de información, pueden ser cualquiera de las

2"

cadenas de n bits. Para

obtener un código de distancia minima

2,

se agrega otro bit llamado el bit de paridod este es cero si hay un número par de unos entre

los

bits de información y

1

en el caso contrario. Esto se ilustra en las dos primeras columnas de la tabla 1

,

para un código con

3

bits de información. Una palabra código de n + l bits vdlida tiene un número par de unos y a este código se le conoce como código de paridad par. También puede construirse un código en el que el número total de unos en una palabra de n + l

bit

sea impar, a este se le conoce como un código de paridad impar y se muestra en la tercera columna de la tabla.

A

estos códigos tambi6n se les conoce como códigos con un

bit

de paridad, ya que cada uno de ellos hace uso de un

bit

de paridad individual.

Los códigos con un bit de paridad no detectan errores en dos bits, ya que cambiar

2

bits no afecta la paridad. Sin embargo,

los

códigos pueden detectar errores en cualquier número impar de bits. Por ejemplo, si se cambian

3

bits en una palabra de código, entonces la palabra resultante tiene la paridad incorrecta y no es una palabra del código. Esto no nos ayuda mucho. Bajo el modelo de error independiente,

los

errores de

3

bits son mucho menos probables que los errores de

2

bits que no son detectables por

lo

que para fines prácticos la capacidad de detección de error de los códigos de paridad un

bit

es útil solo para errores de un bit. Otros códigos, con distancia mínima mayor pueden usarse para detectar errores múltiples.

(12)

I

o1

1

I

o11

o

I

o11 1

I

1 O0

110 1 110

o

110

101 1 101

o

1

o1

100

o

100 1

1 1 1

o

1 1 1 1

1 1 1

'Tabla l . Códigos distancia 2 con tres bits de información

Códigos para corrección de errores y detecci6n de errores múltiples

AI

usar más de

1 bit

de paridad de acuerdo con algunas reglas bien elegidas se puede crear un código cuya distancia mínima es mayor que

2.

Antes de mostrar como puede construirse, veremos como puede usarse tal código para corregir errores individuales o detectar errores múltiples.

Supóngase que un código tiene una distancia máxima de

3.

La figura 4 muestra un fragmento del cubo n para tal código. Como se muestra, existen al menos dos palabras que no son palabras del código entre cada par de palabras del código. Ahora supóngase que se transmiten palabras de código y asúmase que las fallas afectan a lo más un bit de cada palabra de código transmitida originalmente que a cualquier otra. Por

lo

tanto, cuando se reciba una palabra que no sea del código, se puede corregir el error al cambiar dicha palabra recibida por la palabra de código m6s próxima, como lo indican las flechas en la figura. Decidir que palabra del c6digo se transmitió originalmente para producir la palabra recibida se conoce como decodificación, y el hardware que hace esto es un decodificador corrector de errores.

Un código que se usa para corregir errores se llama código corrector de errores. En general si un código tienen distancia mínima 2c+

1 ,

puede usarse para corregir errores que afectan hasta c bits (c=l en el eiemplo precedente).

Si

la distancia mínima del código es 2c+d+ 1, este puede usarse para corregir errores hasta en c bits y para detectar errores hasta en

d

bits adicionales.

Por ejemplo en la figura

5

inciso (a) se muestra un fragmento del cubo n para un código con una distancia mínima

4

(c=

1

y

d=

1).

Los

errores de bit individual que producen las palabras que no pertenecen al código

00101010 y

1 1

O1001 1

pueden corregirse. Sin embargo, un error que produce 1 O1

O001 1

no puede corregirse, porque ningún error de bit individual puede producir esta palabra y uno de dos errores de

2

bits pudo haberlo producido. Así el código puede detectar un error de 2 bits pero no puede corregirlo.

(13)

Cuando se recibe una palabra que no pertenece al código, no se sabe que palabra del código se transmitió originalmente, s610 sabemos que palabra del código es la m6s próxima

a lo que hemos recibido. Por lo que, como se muestra en la figura

(b) un error

de

3

bits puede corregirse con un valor incorrecto. La posibilidad de cometer esta clase de error puede ser aceptable si es muy improbable que ocurran estos errores de

3

bits. Por otra parte, si esta interesado por errores de

3

bits, puede cambiarse la política de decodificación para el código. En vez de tratar de corregir errores, sólo se marcan todas aquellas palabras como errores irrecuperables. Por lo que, como se muestra en (c), puede usarse la misma distancia

4

para detectar hasta

3 errores de bits, pero sin corregirlos (c=O,

d=3)

/-ó-

om1010

1001011/ 1

010101 ~ / o m m 1 1

O01 101 1

-

1 1 1

Palabra de código

Palabra que no pertenece al código

'Figura 4. Algunas palabras código no lo son en un c6digo de 7 bits con distancia 3

(14)

Errores de 2 bits detectables

/

j

',

de 1 a 3 bits

'Figura 5. Palabras de código y otras que no lo son en un código de 8 bits distancia 4: (a) correcci6n de errores de 1 bit y detecci6n de errores de 2 bits; (b) "corrección" incorrecta de un error de 3 bits; (c) no hay corrección pero se detectan errores hasta de 3 bits.

(15)

Cbdigos de Hamming

En

1950,

R.

W.

Hamming describió un método general para construir códigos con una distancia mínima de

3,

ahora llamados códigos de Hamming. Para cualquier valor de i, su método da un código de

2'

-1

bits con i bits de paridad y

2'-1

-i bits de información. Se obtiene códigos de distancia

3

con un número más pequeño de bits de información al suprimir bits de información de un código de Hamming con un número mayor

de

bits.

Las posiciones de los bits en una palabra código

de

Hamming están enumeradas de

1

a

2'-1.

Cualquier posición cuyo número sea una potencia de

2

es un bit de paridad, y las restantes posiciones son bits de información. Cada bit de paridad se agrupa con un subconjunto de

los

bits de información según se especifica con una matriz de verificación de

paridad. Como se muestra en la figura

6

inciso

(b), cada bit

de

paridad se agrupa con

las

posiciones de información cuyos números tienen un

1

en el mismo bit cuando se expresan en binario. Por ejemplo, el bit de paridad 2

(O1

O)

se agrupa con

los

bits de información 3(01

l),

6(

1

1 O)

y

7 (

1 1 1).

Para una combinacibn dada de valores

de

bits de información, cada bit de paridad se elige para que en el número total de unos en su grupo sea par.

Posición del bit

7 6 5 4 3 2 1

~~

. ~ ~,

C

7 6 5 3

C '

4 2 1

P I

'Figura 6. Matrices de verificaci6n de paridad para códigos Hamming de 7 bits: (a) con las posiciones de los

bits en orden num6rico; (b) con bits de paridad y de información separados.

(16)

Tradicionalmente, las posiciones de bit de una matriz de verificación de paridad y las palabras de código resultantes se recomiendan para que todos los bits de paridad estén a la derecha, como en la figura 6 inciso

(b).

Las primeras dos columnas de la tabla

2

presentan las palabras de código resultantes.

Puede probarse que la distancia mínima de un código de Hamming es

3

al probar que deben cambiarse al menos

3

bits para que una palabra de código se convierta en otra palabra del código. Esto es, se probara que un cambio de 1 o

2

bits en una palabra de código no da una palabra del código.

Si

se cabía un

bit

de una palabra de código, en la posición, luego se cambia la paridad de cada grupo que contiene la posici6n. Ya que cada bit de información esta contenido a1 menos en un grupo, al menos un grupo tiene paridad incorrecta y el resultado es una palabra incorrecta.

iQué sucede si se cambian dos bits, en la posición j y

k ?

Los grupos de paridad que contengan ambas posiciones j y

k

aún tendrán paridad correcta, ya que la paridad no se

afecta cuando un número par de bits se cambia. Sin embargo, ya que j y

k

son diferentes, su representación binaria difiere en al menos un

bit,

correspondientes a uno de los grupos de paridad. Este grupo tiene sólo un bit cambiado, resultando una paridad incorrecta y una palabra que no pertenece al código.

Si se entendió esta prueba, también debe verse como las reglas de numeración de las posiciones para construir un código de Hamming son una consecuencia simple de

'Tabla 2. Palabras códigos en códigos de distancia 3 mínima y de Hamming con 4 bits de información.

(17)

la prueba. Para la primera parte de la prueba (errores de un bit), se requiere que los números de posición sean diferentes de cero.

Y

para la segunda parte (errores de 2 bits), se requiere que dos posiciones no tengan el mismo número. Por lo que, con un número i de posiciones, puede construirse un código de Hamming con hasta

2'-1

posiciones de bits.

La prueba también sugiere como puede diseñarse un decodificador corrector de errores para una palabra de código de Hamming. Primero, se verifican todos los grupos de paridad; si todos tienen paridad par, se supone que la palabra recibida es correcta. Si uno o más grupos tienen paridad par, entonces se supone que ha ocurrido un error individual.

El

patrón de grupos que tienen paridad par (llamado el sindrome) debe coincidir con una de las columnas de la matriz de verificación de paridad, se supone que la correspondiente posición del bit contiene el valor incorrecto y se complementa. Por ejemplo, usando el código definido por la figura

6

inciso

(b) supóngase que se recibe la prueba

O1

O101

l .

Los grupos

A

y

B

tienen paridad impar, correspondiente a la posición

6

de la matriz de verificación de paridad (el síndrome es

1 1

O,

o

6).

AI

complementar el bit en la posición 6 de la palabra recibida, se determina que la palabra correcta es

O001

O1 1

.

Un código de Hamming de distancia

3 puede modificarse fácilmente para incrementar

su distancia mínima a

4. Sólo

agréguese otro bit de paridad, elegido para que la paridad de todos los bits, incluyendo el nuevo, sea par. Como en el código de paridad par de

1

bit, este bit asegura que todos los errores que afecten a un número impar de bits sea detectable. En particular, cualquier error de

3

bits es detectable. Ya se demostró que errores de

1

y

2

bits se detectan por otros bits de paridad, así que la distancia mínima del código modificado debe de ser

4.

Los códigos de Hamming de distancia

3

y

4

comúnmente se usan para detectar y corregir errores en las memorias de las computadoras, especialmente en las grandes

computadoras en las que ocurre la mayor parte de las fallas en los circuitos de la memoria. Estos códigos son especialmente atractivos para palabras anchas de memoria, ya que el número requerido de bits de paridad crece lentamente con el ancho de la palabra de memoria. Como se muestra en la tabla 3.

Bits de Códigos distancia

3

mínima C6digos distancia 4 mínima

informacibn Bits de paridad Total de bits Bits de paridad Total de bits

1 2

- <16 5

5 15 4

1 1 1

5 8 4 1 7 3

1 4

4 3 3

I 2 6

I 128

8 I 1 2 7

7

5 120

I 6 4 7

5 63 6

157

I 3 2 6

5 3 1 5

~~~ ~~

'Tabla 3. Longitud de palabras en códigos de Hamming de distancia 3 y 4 .

(18)

Códigos de suma de verificación

La operación de la verificación de la paridad que se ha usado en las subsecciones previas son esencialmente sumas modulo

2

de bits, la suma módulo

2

de un grupo de bits es

O

si el número de unos en el grupo es par, y

1

si éste es impar. La técnica de suma modular puede extenderse a otras bases distintas de

2

para formar dígitos de verificación.

Por ejemplo, una computadora almacena información como un conjunto de bytes,

8

bits. Cada

bit

puede considerarse que tiene un valor decimal entre

O

y

255.

Por

lo

que podemos usar suma módulo

256

para verificar

los

bytes. Formamos un byte de verificación individual, llamado suma de verificación, esto es, la suma módulo

256

de todos los bits de

información.

El

código como suma de verificación resultante puede detectar cualquier error de un byte, ya que tal error ocasionará que la nueva suma de los bytes difiere de la suma de verificación.

Un código con suma de verificación puede combinarse con un código de paridad impar de un

bit,

para formar un código corrector de errores, de distancia 4, bidimensional para un sistema de memoria de computadora.

Códigos m de n

Los

códigos

1

de n y m de n que se mencionaron anteriormente tienen una distancia mínima de

2,

puesto que cambiar un sólo bit cambia el número total de unos en una palabra de código y por tanto se produce una palabra que no pertenece al código.

Estos códigos tienen una propiedad de detección de error útil, la detección de errores múltiples unidireccionales. En un error unidireccional, todos los bits erróneos cambian en la misma dirección (los

“O”

cambian a “ 1 ” y viceversa). Esta propiedad es muy útil en sistemas donde el mecanismo de error predominante tiende a cambiar a los bits a la misma dirección.

BCH

Es una generalización de los códigos Hamming que permiten la corrección de múltiples errores. Estos son una potente clase de códigos cíclicos que proporcionan una gran selección de bloques de longitud, índice de código, tamaño de alfabeto y capacidad de corrección de error.

El

código

BCH

(Bose-Chaudhuri-Hocquenghem) es una de las más importantes clases

(19)

(20)

Codificodor y decodificador corrector de errores Reed-Solomon

C Ó D I G O

R E E D - S O L O M O N

Es un conjunto de estructuras para la corrección de errores con una amplia gama de aplicaciones tales como:

Corrección de errores en dispositivos de almacenamiento (por ejemplo:

Comunicaciones móviles.

Comunicaciones digitales en ambientes ruidosos. Compact

Disk, DVD,

etc.) y para códigos puros.

Descripci6n general

0

El

código Reed-Solomon se describe como

RS(255,255-2t)

con símbolos de

8

bits, otras palabras de código o longitud de símbolos puede ser generados.

0 La palabra código puede ser reducida a

(S, S-2t)

donde

S<255.

0 La paridad sobrepasa sus

2t

símbolos (bytes) por palabra de código. 0 Corrige t símbolos incorrectos en cualquier punto de la palabra código.

La función de codificación

RS

toma cualquier arreglo de

k

símbolos como datos de entrada y regresa a un arreglo de n símbolos (una palabra código Reed-Solomon).

Arquitectura:

0 Codificación y decodificación en el dominio del tiempo

0 Decodificación rdpida usando los algoritmos de Berlekamp-Massey,

Es de alta confiabilidad y eficiencia. búsqueda de Chien y Forney.

1

Code Data Rate

Los códigos Reed-Solomon son un subconjunto de los códigos

BCH

y códigos de bloques lineales. Un código Reed-Solomon esta especificado como

RS

(n,

k)

con S símbolos.

Eiemplo: Un código Reed-Solomon muy popular es

RS(255,223)

con símbolos de

8

bits. Cada palabra decodificada puede contener

255

bytes de palabra código, de los cuales

223

bytes son información y

32

bytes son paridad.

Para este código:

n =

255, k

= 223, S =

8

(21)

M O D E L O D E

U N

SISTEMA

D E C O M U N I C A C I O N E S

La comunicación de datos es el proceso de transferir información digital entre dos o más puntos. La información se define como el conocimiento o forma del conocimiento.

La

información que se procesa y se organiza se llaman datos.

Los

datos pueden ser cualquier información alfabética, numbrica o simbólica, incluyendo

los

símbolos alfanumbricos, etc.(Se mencionaron en la sección Antecedentes). En la fuente y el destino, los datos están en forma digital. Sin embargo, durante la transmisión,

los

datos pueden estar en forma digital o analógica.

En un sistema de comunicaciones, como en una red telefónica, de televisión o de computadoras, etc. Se puede modelar como un diagrama de bloques, como el que se presenta en la siguiente figura.

Tx

F p ) y F ' [x) nunca son iguales

¡(x) = Polinomio de información, palabra, vector etc.

C(x)

= Polinomio, palabra, o vector del código. R(x) = Polinomio, palabra, o vector recibido. E(x) = Polinomio, palabra o vector de error

(22)

La figura

7

nos muestra la relación entre la información de la fuente original, el transmisor, el medio de transmisión, el receptor y la información recibida en el destino.

Un sistema de comunicaciones electrónicas consiste de tres secciones primarias: un transmisor (Tx), un medio de transmisión (canal) y un receptor

(Rx).

El

transmisor convierte la información original de la fuente a una forma más adecuada para la transmisión, el medio de transmisión proporciona un medio de conexión entre el transmisor y el receptor, el receptor convierte la información recibida a su forma original y la transfiere a su destino. La información original puede originarse de una variedad de fuentes diferentes y ser de forma analógica o digital.

Un circuito de comunicación de datos puede ser tan corto, de unos cuantos metros, o tan largo de varios miles de metros; el medio de transmisión puede ser tan sencillo como un pedazo de cable, o tan complejo como un sistema de microondas, satélite o fibra óptica. Por lo tanto, debido a las características, no ideales del canal, que están asociadas con cualquier sistema de comunicación es inevitable que ocurran errores y es necesario desarrollar e implantar procedimientos para el control de errores.

El

control de errores puede dividirse en dos categorías generales: detección de errores y corrección de errores.

Detección de errores

La detección de errores es el proceso de monitorear la información recibida y determinar cuando un error de transmisión a ocurrido. Las técnicas de detección de errores no identifican cual bit (o bits) es erróneo, solamente indican que a ocurrido un error.

El

propósito de la detección de errores no es impedir que ocurran errores, pero previene que los errores no detectados ocurran. Cómo reaccione un sistema a los errores de transmisión, depende del sistema y varia considerablemente. Las técnicas de detección de errores más comunes usadas para los circuitos de comunicación de datos son: Redundancia, codificación de cuenta exacta, paridad chequeo de redundancia vertical y longitudinal y chequeo de redundancia cíclica, etc.

Redundancia

La redundancia involucra transmitir cada carácter dos veces. Si el mismo carácter no se recibe dos veces sucesivamente, a ocurrido un error de transmisión.

El

mismo concepto puede usarse para los mensajes.

Si

la misma secuencia de caracteres no se recibe dos veces sucesivamente, en exactamente el mismo orden, a ocurrido un error de transmisión.

Corrección de errores

(23)

7.

Sustitución de simbolos.- Se diseño para usarse en un ambiente humano: en donde hay un ser humano, en la terminal

de

recepción, para analizar los datos recibidos y tomar decisiones sobre su integridad.

2.

Retransmisión.- Como su nombre lo implica, es volver a enviar un mensaje, cuando es recibido un error, y la terminal de recepción automáticamente pide la retransmisión de todo el mensaje.

3.

Seguimiento de corrección de error.-

El

seguimiento de corrección de error

(FEC),

es el Único esquema de corrección de error que detecta y corrige los errores de transmisión, del lado receptor sin pedir retransmisión.

Con

FEC,

se agregan bits al mensaje, antes de la transmisión. Algunos códigos de corrección de errores son el código de Hamming,

el

BCH,

el Reed-Solomon,

el

Faire Burton, etc.

OBJETIVOS

DE LA T R A N S M I S I ~ N

DIGITAL DE

LA

INFORMACIÓN.

Transmisión fiable (control de errores

)

>

,-

Codificación de canal. Transmisión rdpida

(

compresión

)

Codificación de fuente.

0 Transmisión segura

(

privacidad

)

”-+

-

Criptografía.

C O D I F I C A C I ~ N DEL CANAL

0 Protege la información frente a degradaciones del canal.

0 Añade redundancia de forma inteligente.

(24)

CAMPOS FINITOS {CAMPO D E G A L O I S }

El

Campo de Galois es una aplicación del álgebra de Reed Miller y es una herramienta indispensable para trabajar con los códigos correctores de errores.

Generación de un Campo de Galois (9)

p

es un número primo

Donde q =

p"

; ;

siempre

p

=

2 n

es entero

1 )

El

polinomio primitivo e irreducible del orden n, se representa de la siguiente manera.

P(x)=x"+x+

1 2)

Por ejemplo un polinomio primitivo e irreducible de orden

3.

Campo de Galois

₂₃

(CG (23))

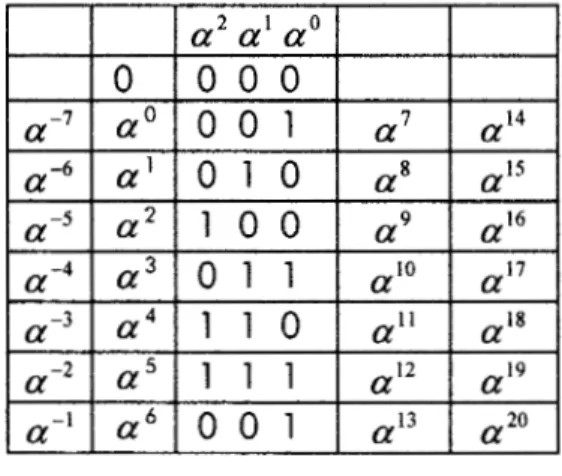
Este campo lo podemos generar a partir de los siguientes pasos:

Para

a3

1) x =

a

en

P(x)

2) P(x)

=

o

P ( ~ ) = o = ~ ~

+a+l

a3

=

a+l

a

= a . a

a4

= a 2

+a

a5 =

a(a2 +a)

= a2

+a3

a 6 = a + a

a 7 = a

+a

4 3

3 4

(25)

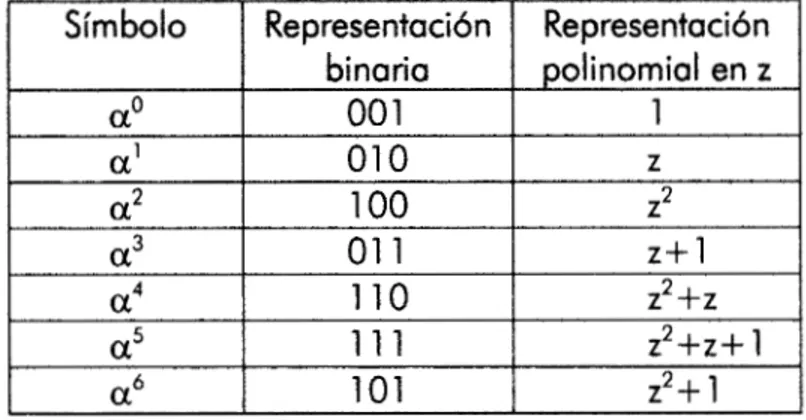
CG(23)

se representa

de

la siguiente manera:

Tabla Campo de Galois (

z3)

(26)

C Ó D I G O

REED-SOLOMON

A

partir de aquí analizaremos el algoritmo teórico del código Reed-Solomon

y

su aplicación en

hardware.

El código Reed-Solomon, es un código detector corrector de errores, al cual se le considera

un

código lineal

(

dado que la suma de

3 palabras del código es una palabra del código), cíclico

y

de

bloque

Algoritmo

Teórico

En

un

código Reed-Solomon (n, k) que corrige t errores, donde n>k;

n

es el número de elementos

de redundancia y k es el número de elementos de información.

La distancia se calcula de la siguiente manera:

d

= 2t

+

1,

t entero

d

2 2e

+

f

+

1

; donde e es el error y no se sabe posición ni valor y f es el borrado en el se conoce la posición pero no el valor

El Campo de Galois se calcula utilizando el polinomio primitivo con un número n aleatorio

KG(2")

}.

Polinomio primitivo e irreducible del orden n

P(x)=x"+x+

1 Calculo

de g(x)

y

h(x).

d-1

g(x)

=

r I ( x -a')

i=l

n

h(x)

=

U(.

- a')

r=d

necesitamos saber el valor de la distancia d para poder calcular e y

f,

dado el número de errores t calculamos d de

la

siguiente forma:

d = 2 t + 1

(27)

d > 2 e + f + l

Por ejemplo:

Dado t =

3,

d

=

7

los valores de e y f pueden ser:

Si

calculamos g(x) y h(x) con el valor de d = 7

i=l

n

h ( x )

=

n ( x

- a')

i=7

El grado de g(x) =

n

-

k

.

Si

consideramos unRS(15,9), sabemos que

n

= 15 y

k

= 9

Codificacibn

r

1

=

c h , C n - + j l ,

donde

i e [ l ,

...,

n - k ]

Canal

En el canal están presentes

E(x)

y

F(x),

donde

E(x)

representa los errores y F(x) representa los borrados por ejemplo:

E(x) = a 2 x l 1 + a 5 x 3 ; donde los exponentes en las alfas ( a ) nos dan el valor del error y el valor de las exponenciales de las x nos da la posición del error.

(28)

Polinomio de erratas

Decodificación

Calculo de Síndromes.

Si

=

(R

=a')

donde

i

~ [ l ,

....,

2t]

Calculo del polinomio localizador de borrados z(x)

c

Calculo de

los

síndromes de Forney,

T(x)

T(x) =

[(1+

S(x))z, (x)

+

11

mod

x d

Algoritmo de Berlekamp (calculo de ( ~ ( x ) )

(0)

cT(x) =

1,

e ,

=o,

do =

Tf+,

I para

n

=

O,

m

= -1

formula de discrepancia:

Existen dos casos:

Caso

1 .-

@+I) (n)

Si

d, = O

,

entonces o(x) =a(x) y

e,+,

= - e n I donde n es la variable que incrementa.

caso

2.-

(n+U (n) ( m )

Si

d,

z

O I entonces ~ ( x ) = a(x)- d,d:x"-m o(x) y n+l =

max{t,,f,

+

n

-

m}

el valor de m

(29)

1)

- l l m < n

2)

d m

# O

3)

m

- sea

máximo.

Esto continua hasta que:

n

<

t

+l.+,

-1

-[

$1.

Calculo de las raíces inversas de a(x) / búsqueda de Chien.

Este calculo se obtiene evaluando a(x) para x = a"donde

i

es la posición

del

error de

E(x)

-

Calculo de valores de erratas.

a) Polinomio evaluador de erratas

R(x).

R(x)

=

(1

+

T(x)k(x) mod

X d

XJ+f

"R(x;')

n(.,;y1-

b)

Calculo de valores de erratas

YJ

= ; j E

[l,(e+

y)],

donde x j son

los

'fJ

errores de borrados.

Ejemplo práctico con un

RS(7 5,9

1,

donde y1 = 15 y

k

= 9.

Sea :

i(x) = a 6 x 7

+

a 9 x 6

+

a 3 x 2

+

al3

~ ( x ) = a 9 x I 4

+

a'Ox

~ ( x )

=

a 14 11 x + a 0 x 7

Para

t

=

3

errores, la distancia d =

2t

+ 1

I es d = 7 I se debe cumplir que:

d > 2 e + f + l

Ahora al sustituir d = 7 la formula queda

de

la siguiente manera:

(30)

La siguiente tabla muestra los valores posibles que pueden ser tomados por e (error) y

f

(borrado) para poder satisfacer la desigualdad anterior.

Una vez determinado el par de valores, el siguiente paso es el calculo de g(x)

o

h(x)

,

en este ejemplo mostraremos el calculo de h(x)

.

Iniciamos calculando h(x) con la siguiente ecuacibn

n

h(x) = n ( x

-

a‘)

i=d

como

n

= 15 y

d

= 7

,

entonces

15

h(x) = n ( x -

a ’ )

i=7

desarrollando la ecuacibn

h(x) = (X

-

a 7 ) ( x -

a ’ ) ( ~

- a9)(x

-

~ ‘ O ) ( X

-

CZ”)(X -

a ” ) ( ~

-

CZ”)(X -

a “ ) ( ~

-

a’,)

después de realizar todas las multiplicaciones encontramos que

h(x) =

x 9

+

a ” x 8

+

d 2 x 7

+

a

x6

+

a 8 x 5

+

a 4 x 4

+

a 4 x 3

+

a 7 x 2

+

aI2x

+

a9

donde:

h,

= a

h,

= a

h2 = a

h,

= a

h, =al2

h,

= a

9 8

I 12

(31)

xn-ki(x) =

x 6 ( a 6 x 7

+

a 9 x 6

+

a 3 x 2

+

a l 3 ) =

a6xI3

+

a9xI2

+

a 3 x 8

+

aI3x6

a partir de aquí obtenemos los siguientes valores de

C ( x )

C13

=

a6

c,,

= o

C,

= a l 3

C,, = O

C,

=

O

c,,

=

a9

C,

=

a3

los valores faltantes de

C ( x )

se encuentran con:

9-1

c6+ = hjC15-,-j

j=O

Para i = l

C,

=

hocl4

+

h,c13

+

h2C12

+

h3Cl,

+

h4Clo

+

h5C9

+

h6C8

+

h,C7

+

h8C6

= a

12

a

6

+ a 7 a 9 + a a 3 + a

10

a

13

= a 3

+a’ +a4 +a8

= a 6

Para i = 2

C ,

=

hocl3

+

h,cl2

+

h2Cll

+

h,Clo

+

h4C9

+

h,C8

+

h6c7

+

h7C6

+

kc5

= a

12

a

6

+ a 7 a 9 + a a 3 + a

10

a

13

= a 3 + a 1 + a 4 + a 8 = a

6

3 C,

=

hoc,,

+

h,Cl,

+

h2ClO

+

h3C9

+

h4C8

+

h,C,

+

h6C6

+

h7C5

+

h8C4

= a 9 a 9 + a 4 a 3

+aaI3+a

12

a

6

+ a

10

a

5

= a 3 + a 7

+al4

+ a 3 + a o = a 4

Para i = 4

C ,

=

h o c l l

+

h,Clo

+

h2C9

+

h3C8

+

h4C,

+

h5C6

+

h6C,

+

h,C4

+

h,C3

= a 4 a 3 + a a

8 13

+ a a 6 + a

12

a

5

+ a

10

a

4

(32)

Para i = 5

C,

=

hoC,,

+

h,C9

+

h2C,

+

h3C7

+

h4C6

+

h,C,

+

h6C4

+

h7C,

+

h,C,

= a 7 a 5 + a a + a 8 a 6 + a a 5 + a a + a

a

= al0

+ a 2

+ a ' 4 +a6 +a+a"

= a

4

4 13 12 4 10 o

Para i = 6

C,

=

h o c ,

+

h,C,

+

h2C7

+

h,C6

+

h4C,

+

h,C4

+

h6C3

+

h7C2

+

h,C,

= a

a +a

a

+ a 4 a 6 + a g a 5

+ a a 4 + a

a + a

a

=a0

+ a 2

+a'' +al3 +a5 +al2

+al4

= a

12

12 3 4 13 12 o 10 4

~ 1 =a6 3

C ,

=ao

C,

= O

c,,

= a 9

C,

= a 4

C,

= a

3

c,,

= o

c,

=a13

c,

= a 4

C,,

= O

C,

= a 6

C,

=al2

Tabla de valores de

C ( X )

completa.

C ( X )

=

a6xI3

+

a9xI2

+

a 3 x g

+

aI3x6

+

a 6 x 5

+

a 5 x 4

+

a 4 x 3

+

a o x 2

+

a 4 x

+

al2

Polinomio de erratas

p ( x )

=

~ ( x )

+ F ( x )

=

a9xI4

+ a

14

x

1 1

+

a 0 x 7

+

al'x

(33)

S, =

a9aZ8

+

a6a26

+

a9a24

+

ai4a22

+

a3ai6

+

a0a'4

+

a13a',

+

a6a" +aja8

+

a4a6

+

a0a4

+

a2a2

+

al2

S ,

= a 7 + a 2 + a 3 + a 6 + a 4 + a ' 4

+a" +a' +al3 +a" +a4 +a4

+a" = a o

S, =

a9a4=

+

a6a39

+

a9a3,

+

a'4a33

+

a3aZ4

+

a0a2' +a"a"

+

a6a'5

+

a5a12

+

a4a9

+

aoa6

+

a2a3 +a'?

S 3 -

-a5' +a4' +a45

+a4' +a2'

+a2' +a3' +a2' +a'? +a'3 +a6 +a5 +aL2 =al4

S(X) = a 4 x 6

+

a 4 x 5

+

a12x4

+

a I 4 x 3

+

a o x 2

+

a'Ox

Calculo de polinomio localizador de borrados

f

z(x) = n ( x - x,) = ( x - d l ) ( x

-

a ' ) ; donde

los

valores de x, son datos

del

borrado

F(X)

j = 1

= x2 -(a11 +a7)x+a18 = x 2 + a 8 x + a 3

invirtiendo

z ( x ) = a 3 x 2 + a 8 x + 1 donde

z2

= a 3 , z, = a 8

,

z = a O

,

Calculo de los síndromes de Forney

d=7,

t=3.

(34)

a 4 x 6

+

a'lx'

+

a12x4

+

a14x3

+

a o x 2

+

a l o x

+

1 a 3 x 2

+

a'x

+

1

a 7 x g

+

a14x7

+

aI6x6

+

aI7x5

+

a 3 x 4

+

d 3 x 3

+

a 3 x 2 a'2x7

+

aI9x6

+

a20x5

+

aZ2x4

+

a 8 x 3

+

aI8x2

+

a ' x

a4x6 +al1x5 +a12x4 +a4x3 +aox2 +a"x+l

a 7 x 8

+

a 5 x 7 + a o x 6 + a 6 x 5 + a 6 x 4 + a 0 x 3 + a o x 2 + m + I

por lo tanto tenemos

T(x) = a o x 6

+

a 6 x 5

+

a 6 x 4

+

a 0 x 3

+

a o x 2 + m

Calculo de a(x) polinomio de Berlekamp

Para

n =

O

do

=

T3

=

1 ~ ( x ) = 1 d-, =

1

(-1) _{a ( x ) = l}

m=-1

(35)

k'2=m~{l,0+1-O}

C , = 1

donde n<3+1-1-

[:I

~~ 3 1 < 2 comosecumplese

continua con el algoritmo.

Ahora para n = 2 , m = O

d,

=a6

+a6(a6)=a6

+a"

= a 4

(3) (2) ('o)

a(.) = a(x)- d,di1x2 a(x) = 1

+

a 6 x

-

a 4 x 2

(3 )

o(x) = a 4 x 2

+

a 6 x

+

I

t 3

= max{1,0+ 2

-O}

=j . e 3 = 2, 2

c

3

+

2 - 1

-

1,

2 <

3,

por

lo

que se continua con el algoritmo.

Para

n

=3,

m

= 2

d3

=a0

+a6a6

+a6a4

=a0

+a"

+al0

= a

14

(4) (3) (2)

a(x) = a(x) - d3di1x a(x) = a 4 x 2

+

a 6 x

+

1 -

a'4a-4x(l

+

a'x)

= a 4 x 2 + a 6 x

+

1 -al0x

+

a16x2

(4)

a(x) = a o x 2

+

a 7 x

+

1 t 4

=max{2,1+3-2} a . e 4 = 2 ,

n < t + t , , + l - l -

[i],

3<3+2-1-1, 3 3 < 3

nosecumple

por

lo

tanto se termina con el algoritmo y

(36)

Calculo de las raíces inversas de a(x), búsqueda de Chien

Para encontrar las raíces inversas a(x) =

a(a")

/ es decir

la

potencia de acorresponde

al

valor de las potencias de las x de E(x)

.

E(x) = a9x14

+

al0x I donde x1 = al4 y x2 =

a

son las posiciones de los errores.

Calculo de erratas Q(x).

Q(x) = (1

+

T(x))o(x)mod x d , d =

7

a o x 6

+

a 6 x 5

+

a 6 x 4

+

a 0 x 3

+

a o x 2

+a

x

+

1 a o x 2

+

1

a o x 8

+

a6x7

+

a 6 x 6

+

a 0 x 5

+

a 0 x 4

+

a'x3

+

a o x 2

a7x7 +a13x6 +a13x5

+

a 7 x 4 + a 7 x 2 + a 8 x 2 + a 7 x a o x 6

+

a 6 x 5

+

a 6 x 4

+

a 0 x 3

+

a 0 x 2

+a

x

+

I

a o x 8

+

a10x7

+

ox6

+

ox5

+

a 5 x 4

+

a 3 x 3

+

a 8 x 2

+

a14x

+

1

~ ( x ) = a 5 x 4

+

a 3 x 3

+

a o x 2

+

a14x

+

1

Calculo de

los

valores de erratas de

Yd

donde

x1 = a x3 = a

x2

= a

x4

= a

xj

[

14

(37)

~ ( a l ~ ) = a

a + a a + a a + a a +I

=asa1' + a a + a a

+a28

+I

=a' +ao + a 6

+a'3

+ao = a 4

5 56 3 42 8 28 14 14

3 12 8 13

Y , = a a

6 4 = a 10

y 2

=

al2

- - -

n(a-14)=

a3n(a>

= al3 [,'a4

+

a3a3

+

a8a2

+

al4a

+

11 al4

y 2

= a 9 [ a 9 + a 6 +alo +ao + a 0 ] = a 9

y 3

= --~(a8)= a6

a13

+

a3a24

+

al4aS

+

a O ]

a8

y3 =al3[a7

+al2 + a 9 + a 7

+ao]=al5

= a O

y4

= - ~ n ( a ~ ) =

a3

a 3

T [ a

5 a 16 + a 3 a 12 + a 8 a 8 + a 14 a 4 + a 0 ]

(38)

Y , =a9(a6 + a o + a 1 + a 3 + a o ) = a

9

a

5

= a

14

Los resultados se resumen en la siguiente tabla:

I

Y ,

=

alo

I

x , = a

1

_a'Ox

1 Y ,

= a

x2

= a

a9xI4

Y3

= a

x3 = a

a0x7

9 14

O 7

I

y4

=

al4

I

x ,

=

al1

I

al4xl1

I

Finalmente

p ( x )

=

a'Ox

+

a9x14

+

a0x7

+

a

14

x

11

(39)

I M P L E M E N T A C I Ó N EN

HARDWARE

D E UN CODEC CORRECTOR DE

ERRORES REED-SOLOMON

Nuestro codec Reed -Solomon

(7,3)

se compone de las siguientes tres etapas:

1.

Codificador

2.

lnterfaz

3.

Decodificador

CODIFICADOR

Para implementar el diseño del codificador en hardware, el primer paso es obtener

h(x)

o g(x) en este caso se obtendrá g(x)

.

g(x) =

gmxm

+

gm_,xm-l

+

...

+

g,x

O

representado gráficamente de la siguiente manera.

3 bits

i(x1 "-/L I

Figura 8. Representación de g(x) = gmxR

+

gm-,xm"

+

...

+

goxo mediante un filtro IIR

Para el codec Reed-Solomon

(7,3)

se trabajo sobre el Campo de Galoa

8 (GF(23)),

la

tabla